Product-Market Fit is Lindy
The longer you search for product-market fit, the less likely you will find it.
This phenomenon is called the Lindy effect.
To be "Lindy" means the longer something survives, the more time it has left. Remaining life extends, rather than contracts, with age.
Perishable objects like flesh-and-blood humans don't work this way. As we age, our remaining time on this Earth decreases — a 90 year-old has less expected time left on the clock than an 80 year-old.
But certain non-perishables follow a different rule. Per Wikipedia:
The Lindy effect is a theory that the future life expectancy of some non-perishable things like a technology or an idea is proportional to their current age, so that every additional period of survival implies a longer remaining life expectancy. Where the Lindy effect applies, mortality rate decreases with time.
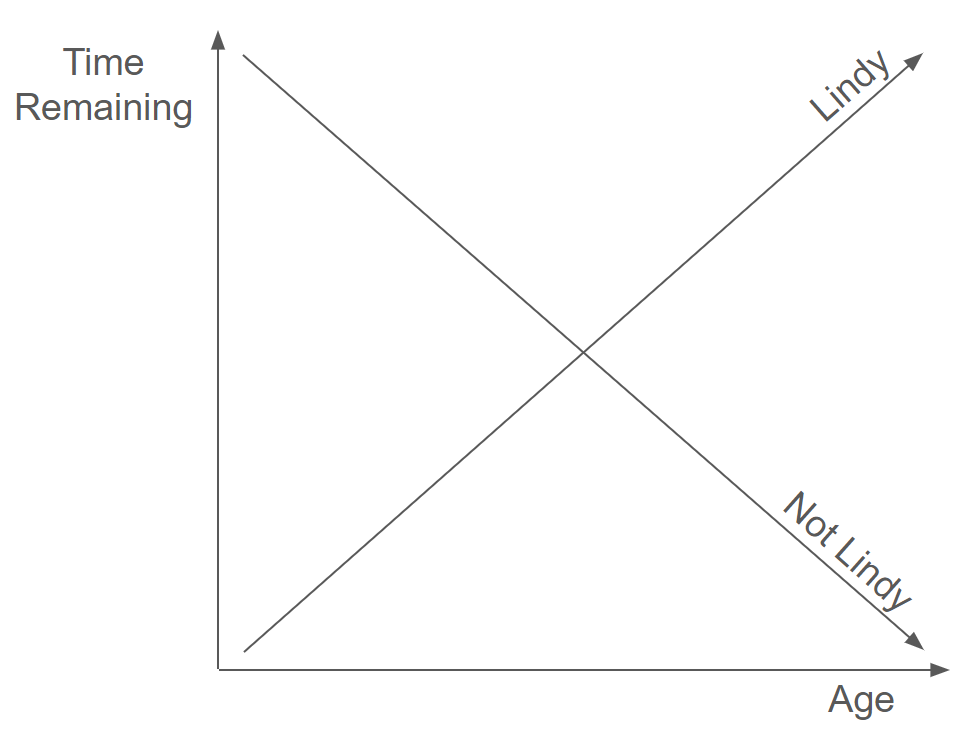
Product-market fit follows the Lindy effect.
More precisely, lack of product-market fit is "Lindy". The longer you don't have it, the longer you won't have it.
An additional year of "no product-market fit" implies a longer remaining period of "no product-market fit." The odds of achieving product-market fit with any particular idea decline with time. Thus, if you don't achieve product-market fit quickly, you may never achieve it at all.
Product-market fit, like the elusive "cure" for cancer, is not a fixed destination, guaranteed to be reached with enough time spent running toward it. In a weird way, moving "toward" it doesn't actually get you any closer to it — it only moves further away.
Product-market fit escapes from you.
Receive my next long-form post
Thoughtful analysis of the business and economics of tech
Product-market fit isn't normal
I was inspired to write this essay by a recent tweet by Matt MacInnis, COO of Rippling, where he claimed product-market fit is obvious once you have it, suggesting business performance is lognormally distributed vis-a-vis product-market fit:
(1) It's been said, but now I get it in my gut: if you have to ask whether you’ve found product-market fit, you haven’t. Like most things, it’s lognormal: better PMF yields way, way better biz performance. At a certain point, most assumptions about how to build a co. break. 2/7
— Matt MacInnis (@stanine) August 4, 2020
No, he didn't mention the Lindy effect directly, but that's what instantly came to mind as I read the tweet.
Here's why.
A lognormal distribution is one which, if you take the logarithm of all its possible values, yields a normal distribution. Hence "log" "normal". Due to the exponential nature of the logarithm, lognormal distributions are skewed:
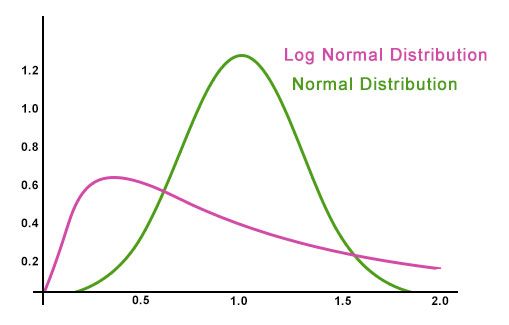
Lognormal distributions are neither normally distributed nor thin-tailed. Instead, they are fat-tailed.
This is an important fact.
When MacInnis says performance is lognormal, or skewed, with respect to product-market fit, he's making the point that, once you have product-market fit, you go straight to the tails. Business performance accelerates so meaningfully that any ambiguity goes out the window. You get it "in your gut." It becomes obvious, as nearly everything about the business gets better.
A/B testing with fat tails
In Why Don't VCs Index Invest, I make the point that, when facing sufficiently fat-tailed distributions, it makes sense to spread your bets widely, avoiding concentration or dependence on any one investment or opportunity. Instead "index invest," placing small bets in everything reasonable without overthinking it too much.
This extends to all domains where fat-tails reign. A fascinating paper by researchers at Microsoft, HomeAway, Wharton, and Columbia University applies this logic to the domain of internet search engines and reaches similar conclusions.
Search platforms like Microsoft Bing and Google face a trade-off when A/B testing various changes:
- run large, data-hungry experiments to get precise effect estimates for potential improvements to the platform
- run small, "lean" experiments that do not have much statistical power but nevertheless detect effects if they are large enough
The conventional wisdom is that larger A/B tests are better because they increase statistical significance of the experimental results, building confidence that seemingly positive results are, in fact, positive.
It turns out, the optimal choice for how many users to assign to an experiment depends on the fat-tailedness of the distribution of potential returns, or what the researchers call, the "innovation value distribution":
... with sufficiently fat tails, this conventional wisdom reverses and the go lean approach of trying many small experiments is preferred. Intuitively, with sufficiently fat tails, even small experiments are sufficient to detect the largest effects; which in this case account for most total value. Larger experiments detect subtler effects, but these constitute less of the total value; making the value of information concave. This case also has different implications for the marginal value of information.
To translate — when most of the potential gains come from a small number of experimental changes (i.e., innovation is fat-tailed), you're better off running as many experiments as possible so as not to miss the potential "big one." Yes, this might come at the cost of statistical precision, but large effects are so large they can be detected even in small samples.
Another way to think about this is in terms of the "value" of information:
while the production function is always concave for large numbers of assigned users, its shape with few users depends critically on the thickness of the tails of the prior. If the prior is not too fat-tailed... then the production function is convex. However, we show that if the prior is very fat-tailed... the production function is concave.
Again, I translate — when the value of experimentation is fat-tailed, the marginal value of additional information declines as you gather more data because any large, positive innovation is easily detectable with only a small amount of data. Thus, collecting more information doesn't help much — the value of information is concave.
On the other hand, if the value of experimentation is normally distributed or thin-tailed, then there are almost no mammoths out there to find. Instead, most innovations are of middling value. In that range, precision matters, as it can be the difference between accidentally implementing a slightly worse change over a somewhat better one. More information helps decipher between the two. Thus, the value of information is convex.
We can see this in the chart below from the Bing paper, which shows the shape of the experiment "production function" (which effectively represents the value of experimentally gained information) when graphed against experiment sample size. The different lines represent various levels of \(\alpha\) , or the assumed fat-tailedness of the innovation distribution. Lower \(\alpha\) means fatter tails, and vice versa.
Fat-tailedness (small \(\alpha\)) leads to a concave information value curve, whereas thin-tailedness (high \(\alpha\)) leads to a convex information value curve:
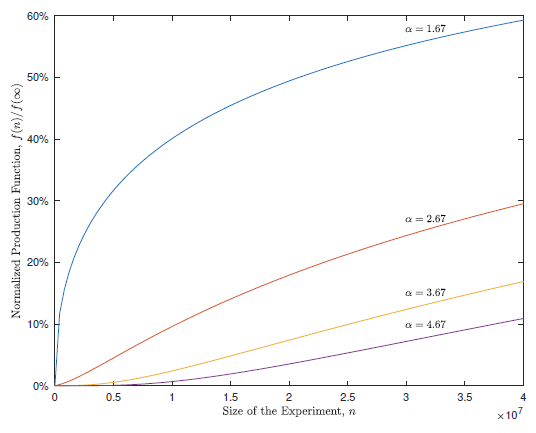
You'll know it when you see it
So which is it?
We present evidence—using a sample of approximately 1,505 experiments—suggesting that innovations at Microsoft Bing have very fat tails.
The innovation value distribution is fat-tailed. So small experiments can detect the largest effects, which represent most of the value of A/B testing:
If the distribution of innovation quality is sufficiently thick tailed, a few ideas are large outliers, with very large negative or positive impacts. These are commonly referred to as black swans, or as big wins when they are positive. The production function is concave and has an infinite derivative at n = 0. The optimal innovation strategy in this case is to run many small experiments, and to test all ideas.
OK, but what does A/B testing with fat tails have to do with product-market fit?
Think about the search for product-market fit as a sort of multifaceted A/B test. You try various permutations of the product, business, and go-to-market model, looking for something that especially resonates with users or customers. The vast majority of these combinations won't work out, but a handful will. Those few will work so well in fact that they will dwarf the performance of all the other iterations.
If it is true that product-market fit yields much better business performance, then product-market fit should be relatively obvious, even with little data. This suggests that, if you do have some data for an idea and it still isn't obvious to you whether or not it achieves product-market fit, you may have a problem, especially if you've been at it for a while.
But isn't that exactly what MacInnis said?
"If you have to ask whether you've found product-market fit, you haven't."
The Bing experiments provide the mathematical and empirical justification for MacInnis' bold statement. While I won't quibble over whether business performance is lognormal or some other distribution, it's clearly quite skewed, just as in the Big experiments. In that kind of world, product-market fit loses much of its mystique — it doesn't take a genius to know whether you have it:
Consider a startup firm that uses a lean experimentation strategy. The firm tries out many ideas in small A/B tests, in hopes of finding one idea that is a big positive outlier. Even though the A/B tests are imprecise, the firm knows that, if a signal is several standard errors above the mean, it is likely to be an outlier. So the firm decides to only implement ideas that are, say, 5 standard errors above the mean. This means that the firm will almost certainly detect all outliers that are more than, say, 7 standard errors above the mean.
"You'll know it when you see it" rings quite true.
Due to fat-tailed business performance, it doesn't take much data to know you've achieved product-market fit, nor does it require some complicated, made-up framework from a supposed startup guru. In the context of the Bing analysis, any A/B test that yielded a result more than several standard deviations above the baseline essentially achieved "fit," with a high degree of certainty.
Starting over
Let's end by returning to where we began — the Lindy effect.
MacInnis' statement is effectively a rephrasing of the Lindy effect — if it's taken long to find product-market fit, it's likely going to take a lot longer.
To rephrase once more: since it doesn't take much data to know you have product-market fit (assuming you do, in fact, have it), then if you haven't achieved it yet, you probably have a long way to go.
This is brutal stuff. However, via lean experimentation, planting many flags in various places and quickly shifting gears when no treasure is found, you can, in expectation, start "closer" to the goal. Per the Microsoft paper:
We call this the "lean experimentation" strategy, as it involves running many cheap experiments in the hopes of finding big wins (or avoiding a negative outlier). This strategy is in line with the lean startup approach, which encourages companies to quickly iterate through many ideas, experiment, and pivot from ideas that are not resounding successes.
I want to emphasize that these are are all probabilistic statements and say nothing about any particular circumstance.
You and your team could have been chasing product-market fit for a given idea for the past year, and, for all anyone knows, it could be just around the corner. Many ideas seemed hopeless and for the longest time didn't work... until they finally did.
But that's not the norm.
Uber, Netflix, Facebook, DoorDash. In each case, soon after launch, it became quite clear they were doing something right. Even in companies that went through many iterations, things started to work very soon after landing on the right idea.
To be clear — the chase does not cause product-market fit to never be achieved. It represents growing evidence it won't be achieved. The chase represents information, the value of which is concave, meaning it has diminishing returns. That one needs to chase at all is, strangely enough, a sign you're on the wrong path.
More viscerally, if the trail through the forest seems much longer than it should be, you're probably lost. Breath, regroup, and try something different.
Receive my next long-form post
Thoughtful analysis of the business and economics of tech